1.1 Interchange Example
1.2 Defining Records Example
1.3 Using InputBox Function Example
1.4 Using MsgBox Function Example
1.5 Finding Min and Max From Two Values First Example
1.6 Finding Min and Max From Two Values Second Example
1.7 Finding Factorial Example
1.8 Finding Min and Max From Two Values Third Example
1.9 Ordering Values Example
1.10 Using If…Then…ElseIf Example
1.11 Extracting Square Root Example
1.12 Determining The Factorial Second Example
1.13 Determining The Easter Date For a Wanted Year Example
1.14 Determining The Factorial Third Example
1.15 Ordering Second Example
1.16 Using For Examples
1.17 Fahrenheit To Celsius Correspondence Table Example
1.19 Working With Matrix Example
COPYRIGHT© 2006-2009 Vasile AVRAM.
This algorithm realize an interchange of the content of the variable named x with the content of the variable y. The variables x and y from the name of the procedure Exchange(x,y) are named arguments and the real value for that are passed to the procedure at call time. The call is realized, in almost algorithmic programming languages (as C ++, Visual Basic, Pascal etc.) by writing the name of the procedure followed by the list of the arguments. The call Exchange(x, y) means applying the operations included in the procedure body to variables x and y.In the computation block from the figure the numbered line means:
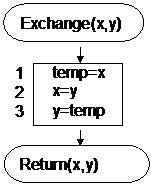
Figure 1 The representation of Exchange operation
|
- (1) the content of variable x is stored in a temporary (working) variable named temp;
- (2) the content of variable x is overwritten by the content of variable y (first is deleted and after deletion the content of y is copied y);
- (3) the content of y is overwritten by those of the variable temp (it contains the value of x as passed at the call time.
The new values of x and y are returned to the caller.
| For example, the call Exchange(3, 2) realizes the operations: |
temp = 3 |
x = 2 |
y = 3 (the temp content) |
And returns 2, 3 |
top
The user defined data type is formed by placing the needed declarative sentences Type block. For example, if we want represent the structure of a row from the Balance_Sheet (the Romanian one) this can be declared by the user as follows:
Type Balance_Sheet_Row
Dim Account_ID As String*22
Dim Account_Description As String*60
Dim Db_Jan As Double
Dim Cr_Jan As Double
Dim Db_Prev As Double
Dim Cr_Prev As Double
Dim Db_Month As Double
Dim Cr_ Month As Double
End Type
After declaration a user-defined data type can be used in the same way data type used. For our example, we can define a memory variable, that we call Current_Row, thus: Dim Current_Row As Balance_Sheet_Row.
You can find other examples of declaring and using user data types (including in other user data type) in:
 Visual
Basic Code Examples
Visual
Basic Code Examples
top
The call InputBox(“Prompt”,”Valoare_implicita”,”Titlu”) will produces the dialog box from figure 2.
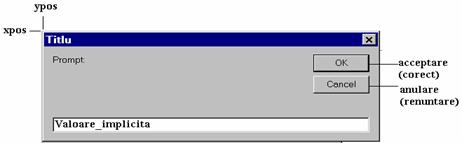
Figure 2 Example of using InputBox |
top
For example the call MsgBox(“Prompt”,vbInformation+vbOkCancel, “Titlu”) will produces the dialog shown in figure 3.
The returned values correspond to the pressed button:
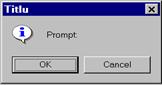
Figure 3 Example of an MsgBox dialog |
Constant |
Value |
Description |
vbOK |
1 |
OK |
vbCancel |
2 |
Cancel |
vbAbort |
3 |
Abort |
vbRetry |
4 |
Retry |
vbIgnore |
5 |
Ignore |
vbYes |
6 |
Yes |
vbNo |
7 |
No |
In the following example is illustrated how to write the message on many lines and what means a string expression:
MsgBox "The Student " & Name & Chr(13) & Chr(10) & " has the average mark: " & media
What is between “…” means literal strings that will be placed as such in the message; Name and media are named variables whose content will be concatenated by the string concatenation operator (&) with the literals and the function calls Chr(13) & Chr(10) means display what follows on a separate line.
top
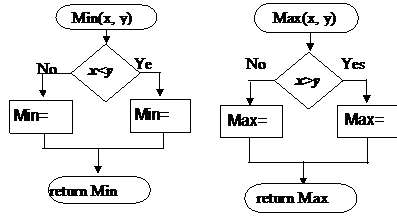
a) b)
Figure 3 A description of min and max algorithms for any kind of data type values
|
We design the logical flowcharts (figure 3) and the corresponding procedures to determine the min value - Min(x, y), and max value - Max(x, y) from two values passed in arguments.
It is possible do not have a specific operation on the two branches, that mean situations as depicted in figure 3. If the condition is true then the set of sentences placed between If and End If are executed.
An implementation of Min and Max
|
Function Min(x As Variant, y As Variant) As Variant
If x > y Then
Min = y
Else
Min = x
End If
End Function |
Function Max(x As Variant, y As Variant) As Variant
If x < y Then
Max = y
Else
Max = x
End If
End Function |
a) Another implementation of Min and Max |
Function Min(x As Variant, y As Variant) As Variant
Min=x
If x > y Then Min = y
End Function |
Function Max(x As Variant, y As Variant) As Variant
Max=x
If x < y Then Max = y
End Function |
This samples looks shorters than the corresponding ones in paragraph 1.5 but is a big difference in how they executes:
- For samples in paragraph 1.5 the execution is done allways in two steps: comparisson followed by an assignment;
- For samples in paragraph 1.6 the execution is done in two (assignment, comparishon) or three steps (assignment, comparishon, assignment), depending on the relationship between x and
y.
top
a) using nested If:
Sub Factorial_Call()
n = InputBox("Type the value for n:", "VB Samples: n!")
If IsNumeric(n) = True Then
If Int(n) = n Then
valReala = Factorial_Iterativ(n)
Raspuns = MsgBox("The Factorial is: " & valReala, vbInformation + vbOKOnly)
valReala = Factorial(n)
Raspuns = MsgBox("The Factorial is: " & valReala, vbInformation + vbOKOnly)
End If
End If
End Sub |
top
We redefine the Min and Max functions by using the procedure Exchange:
Function Min(x As Variant, y As Variant) As Variant
If x > y Then Exchange x, y
Min = x
End Function |
Function Max(x As Variant, y As Variant) As Variant
If x < y Then Exchange x, y
Max = x
End Function |
top
We define a procedure that take as arguments the values of x and y and arrange them in ascending order called Asc(x,y). We do that in two versions: first realize all the operations and the second call the procedure Exchange(x,y).
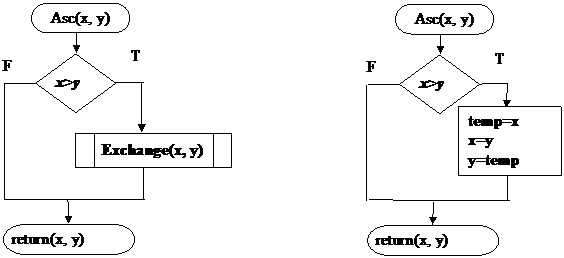
a) b)
Figure 4 The definition of the algorithm for ascending ordering |
In these example the values x and y are arranged (sorted) in ascending order, in conformity with the used comparison operator (< in our case). The algorithm can be conformed to any desired ordering by changing accordingly the comparison operator.
The implementations of the algorithms from figure 4 are:
Sub Asc(x As Variant, y As Variant)
If x > y Then Exchange x, y
End Sub |
Sub Asc(x As Variant, y As Variant)
Dim temp As Variant
If x > y Then
temp = x
x = y
y = temp
End If
End Sub |
top
d) this sequence chooses the case for VAT percent for a VAT calculator:
Private Sub PTvaGen()
If PTva1.Value = True Then
PrTVA = PrTVA1
PTva2.Value = False
Ptvax.Value = False
EtAltTVA.Visible = False
AltTVA.Visible = False
ElseIf PTva2.Value = True Then
PrTVA = PrTVA2
PTva1.Value = False
Ptvax.Value = False
EtAltTVA.Visible = False
AltTVA.Visible = False
ElseIf Ptvax.Value = True Then
PrTVA = PrTVAx
PTva1.Value = False
PTva2.Value = False
EtAltTVA.Visible = True
AltTVA.Visible = True
FrmTva.Refresh
Else
MsgBox "Att.! Computation Error!",vbCritical
End If
End Sub
|
top
Let be a a positive real number. Define recursively the sequence of xi of positive numbers as follow:
x0 = 1
xi+1 = (1/2)*(xi + a/xi) for i=0,1,2,...
Draw a flowchart (figure 5) that reads in the value interactively and uses this algorithm to compute the square root of a (it can shown mathematically that
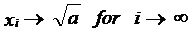 ).
).
The algorithm stops when xi-1 equals with xi-precision, where precision is a positive fraction low value (the desired precision), that mean to be satisfied the following condition |xi-xi-1|≤precision. The condition can be described as: the difference from the current value (xi) and the previous one (xi-1) must be at least the desired precision (for example 0.001 if the precision must be at the third decimal).
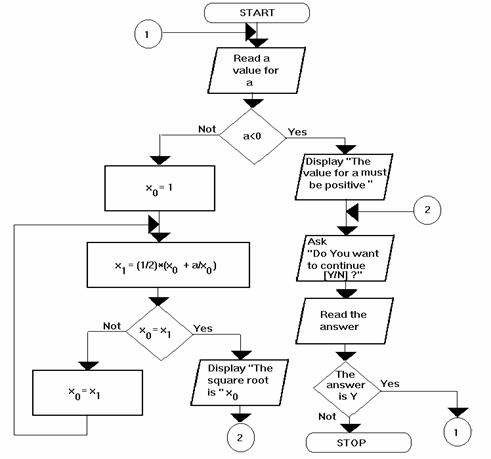 Figure 5 A flowchart for the Newton-Raphson method
Figure 5 A flowchart for the Newton-Raphson method |
This algorithm is derived from the so known Newton-Raphson method in numerical analysis. There is an implementation of the method
(the left main branch in the flowchart) using a form for input-output. The names used in the code are outlined in the form on white background
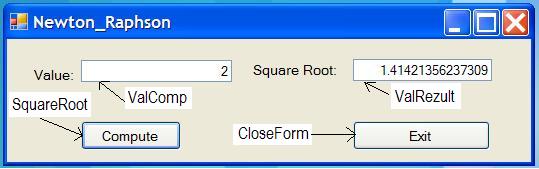
Public Class Newton
Private Sub CloseForm_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles CloseForm.Click
Me.Close()
End Sub
Private Sub SquareRoot_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles SquareRoot.Click
Dim x0 As Double, x1 As Double, a As Double
If IsNumeric(Trim(Me.ValComp.Text)) = False Then
MsgBox("Type a valid value and repeat!", vbOKOnly, "Attention!")
Else
a = Val(Trim(Me.ValComp.Text))
x0 = 1
x1 = 0
Do While True = True
x1 = (1 / 2) * (x0 + a / x0)
If x0 = x1 Then Exit Do
x0 = x1
Loop
Me.ValRezult.Text = x0
End If
End Sub
End Class
top
For a nonnegative integer n the factorial of n, written n!, is defined by:
a) iterative mode |
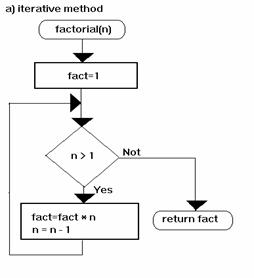 |
0! = 1
n!=n*(n-1)(n-2)*...*3*2*1 for n>0 |
Function Factorial_Iterativ(n As Integer) As Double
Dim fact As Double
fact = 1 ' Initialize to 1 for product
Do While n>0
fact = fact * n
n=n-1 ‘Next cycle
Loop
‘ The returned value
Factorial_Iterativ = fact
End Function |
top
Pope pleases the great mathematician Gauss to tell him when Easter will be in a wanted year. Gauss says that Easter will be always on: 4 April+D days+E days where:
D is determined by following the steps:
1 – the year is divided by 19;
2 – the remainder is multiplied by 19;
3 – to the result of step two add fix factor 15;
4 – the sum of values obtained in the steps 1 to 3 is divided to 30 and the remainder is D
E is determined by following the steps:
1 – the year is divided by 4 and the remainder will be multiplied by 2
2 – the year is divided by 4 and the remainder will be multiplied by 4
3 – compute the sum of values obtained to step 1 and 2
4 – to the sum add 6*D and to product add 6
5 – the total sum is divided by 7 and the remainder will be E
Note: This Formulas Compute The Eastern Date For Orthodox (even Pope is Catholic!)
A code that implements this algorithm is:
Romanian Version: Variables and comments in Romanian language
Sub Date_Pasti()
Dim An_Inceput, An_Sfarsit As Variant, WData As Date
Dim rasp As Byte, i As Integer
An_Inceput = InputBox("Anul de la care " & Chr(10) & Chr(13) & "calculam data Pastelui:", "Calculul datei Pastelui")
An_Sfarsit = InputBox("Anul pana la care " & Chr(10) & Chr(13) & "calculam data Pastelui:", "Calculul datei Pastelui")
For i = An_Inceput To An_Sfarsit + 1
WData = Data_Paste(i)
xExemple.Print i, " ", WData
Next i
ras = MsgBox("Pastele cade in anul " & An_Dorit & " la " & Data_Paste, vbOKOnly, "Calcul data Pastelui")
End Sub
Function Data_Paste(An_Dorit As Variant) As Variant
Dim D As Integer, E As Integer
D = ((An_Dorit Mod 19) * 19 + 15) Mod 30
E = (((An_Dorit Mod 4) * 2 + (An_Dorit Mod 7) * 4) + 6 * D + 6) Mod 7
Data_Paste = DateAdd("d", D + E, CDate("04/04/" & Trim(An_Dorit)))
End Sub
English Version: Variables and comments in English language
Sub Eastern_Dates()
Dim Start_Year, End_Year As Variant, WDate As Date
Dim answer As Byte, i As Integer
Start_Year = InputBox("Year From " & Chr(10) & Chr(13) & " which we compute
Easter date:", "Compute Easter Date ")
End_Year = InputBox("Year To " & Chr(10) & Chr(13) & "to which we compute
Easter date:", "Compute Easter Date")
For i = Start_Year To End_Year + 1
WDate = Eastern_Date(i)
xExemple.Print i, " ", WDate
Next i
answer = MsgBox("The Easter will be in " & Wanted_Year & " ON " & Eastern_Date(Wanted_Year), vbOKOnly, "Compute Easter Date")
End Sub
Function Eastern_Date(Wanted_Year As Variant) As Variant
Dim D As Integer, E As Integer
D = ((Wanted_Year Mod 19) * 19 + 15) Mod 30
E = (((Wanted_Year Mod 4) * 2 + (Wanted_Year Mod 7) * 4) + 6 * D + 6) Mod 7
Eastern_Date = DateAdd("d", D + E, CDate("04/04/" & Trim(Wanted_Year)))
End Sub
top
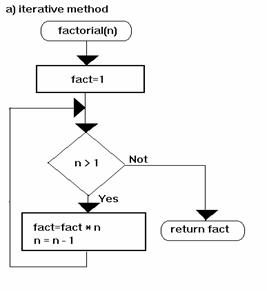
For a nonnegative integer n the factorial of n, written n!, is defined by:
a) iterative mode |
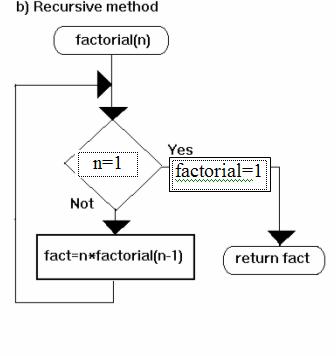
b) recursive mode |
0! = 1
n!=n*(n-1)(n-2)*...*3*2*1 for n>0 |
0! = 1
n! = n((n-1)!) for n>0 |
|
|
Function Factorial_Iterativ(n As Integer) As Double
Dim fact As Double
fact = 1
For i = 1 To n
fact = fact * i
Next i
Factorial_Iterativ = fact
End Function |
Function Factorial(n As Integer) As Double
If n = 1 Then
Factorial = 1
Else
Factorial = n * Factorial(n - 1)
End If
End Function |
top
We realize a generalization of the Asc algorithm so that the values (x and y) are passed together with the comparison operator (relop) that can be '>', '<' and '='. Depending on the value chosen for the comparison (relop) we are the case greater than, less than and otherwise is the equality. The algorithm call the defined algorithm Exchange(x,y) to realize the inter exchange (permutation) of the values, assigned at execution time (run time) to the variables x and y, in the sense defined by the used relational operator (comparison). The algorithm returns the values in the specified order.
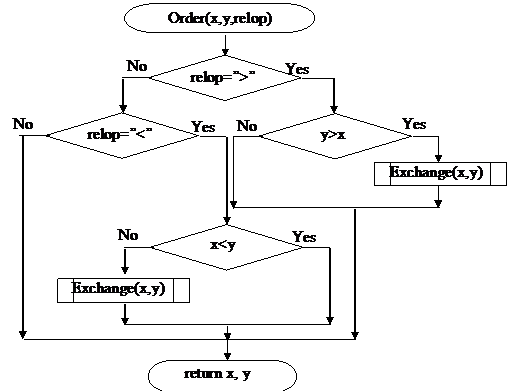
Figure 6 An algorithm for ordering two values |
Sub Order(x As Variant, y As Variant, relop As Variant)
Select Case relop
Case "<"
If x > y Then
Exchange x, y
End If
Case ">"
If x < y Then
Exchange x, y
End If
End Select
End Sub |
This code sequence is a possible implementation of the algorithm explained in the flowchart from figure 6. The declaration of variables as Variant allows using the subroutine Order() to do his action on any kind of data type of the values passed in arguments (text, number, date, etc). The routine can be generalized to receive at input an array, vector or multidimensional massive, or can be called as such from routines that processes such arrays by passing in arguments pairs of values.
top
Given a set of n values v[i], i=1,2,3, …, n.
1.1 Build the function that compute the sum[Sum(v,n)] of this values (a).
(a) The function Sum adds a series v of n numbers
Function Sum(v As Variant, n As Integer) As Double
Sum = 0
For i = 1 To n
Sum = Sum + v(i)
Next i
End Function |
1.2 Build the function that compute the average [Avg(v,n)] of this values (b and b').
(b) The function Avg computes the means of a series of numbers
Function Avg(v As Variant, n As Integer) As Double
Sum = 0
For i = 1 To n
Sum = Sum + v(i)
Next i
Avg=Sum/n
End Function |
(b') The function Avg computes the means of a series of numbers and uses the function Sum defined at (a) point
Function Avg(v As Variant, n As Integer) As Double
Avg=Sum(v,n)/n
End Function |
1.3 Draw a flowchart that exponentiation a number x at the power n [Power(x,n)].
Dissection of the power flowchart (figure 7):
- the Start symbol contains the name of algorithm and the call format. In the brackets is indicated the list of arguments to be passed at call time;
- by i=1 we initialize the counter for the exponent, and we initialize the result to 1 (if n is 0 then x0=1);
- by pow=pow*x we compute the actual value of the variable pow as a multiplication of the previous value of the variable pow with the variable x;
- in the decision block we check how many times we are realized the repeatedly multiplication. If the multiplication is not realized n times we increase the counter and then go to a new multiplication else the algorithm return the result.
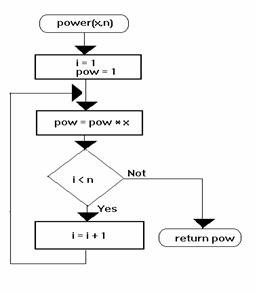
Figure 7 An exponentiation algorithm |
A possible implementation of the algorithm is one of the following:
(a)
' The function Power exponentiation a number x to a power n
Function Power(x As Variant, n As Integer) As Double
Dim pow As Double
pow = 1
For i = 1 To n
pow = pow * x
Next i
Power = pow
End Function |
(b)
' The function Power exponentiation a number x to a power n - compact
Function Power(x As Variant, n As Integer) As Double
Power = 1
For i = 1 To n
Power = Power * x
Next i
End Function |
top
1.17 Fahrenheit To Celsius Correspondence Table Example
We want to solve now a more complex problem: we want to list a Fahrenheit to Celsius correspondence table based on the computation formula:
CELSIUSo = (5/9)*(FAHRENHEITo ‑ 32)
The correspondence table will be displayed (figure 8) starting with the minimal value (min) 0 (zero) and ending with the maximal value (max) of 300 degrees and the computation and display will be done from 20 to 20 degrees (pas). We use, to solve this problem, assignments instructions, the function MsgBox to display the result and an instruction For that allow us to repeat the execution of a group of sentences until a specified condition satisfied.
The program looks as:
0. Sub Coresp_Temp()
1 Dim min, max, pas, fahrenheit#, celsius, tabel
2 ' Computation of the correspondence Co- Fo
3 min = 0 ' Starting Value
4 max = 300 ' Ending Value
5 pas = 20 ' From … to … degrees
6 tabel = "Fahrenheit | Celsius " & Chr(13) & Chr(10) & _
String(36, "-") & Chr(13) & Chr(10)
7 For fahrenheit = min To max Step pas
8 celsius = (5 / 9) * (fahrenheit - 32)
9 tabel = tabel & Right(Space(12) & Format(fahrenheit, "#000"), 12) &_
" " & Right(Space(12) & Format(celsius, "#000.00"), 12) & Chr(13) & Chr(10)
10 Next fahrenheit
11 MsgBox tabel, , "Conversion Fahrenheit-Celsius"
End Sub

Figure 8 The display of Fahrenheit-Celsius correspondence table |
Comments
Line 0 is that in which the type of used procedure and scope declared (public subroutine in our case) together with the name that can be used later on to call the procedure (Coresp_Temp);
Notes ! The numbers associated to the lines can be typed as such in the source program (they keep from previous versions of Basic). The lines that follows after the line numbered 6 and the line numbered 9 are not numbered because they continuation lines of previous sentence.
A continuation is specified by placing an _ (underscore) character to the right of the line.
The writing of many instructions on the same line is also allowed by placing a : (colon) character before each instruction.
Line 1, Dim min, max, pas, fahrenheit#, celsius, tabel declares and reserve the needed memory space. In that line the variables min, max, pas, celsius and tabel, that haven’t a data type specification, are of Variant data type (without a specific data type but adapted to those of the first expression in which is used) and fahrenheit# is a double precision variable;
Line 2 is a comment line introduced by an ' (single apostrophe); his role is to explain the role played by the routine;
Lines from 3 to 5 are assignment statements. What is in the left of the = (called assignment operator) symbol are variable names (min, max, pas). What is in the right represents a constant and/or expression; in that case they are numbers and are called numeric constants. On that lines we define two instructions: one assignment and the second (delimited from the first by ') a comment.
Line 6 is an assignment line that initialize the variable named tabel with a character string, formed by two lines, string obtained by evaluating the string expression "Fahrenheit | Celsius " & Chr(13) & Chr(10) & String(36, "-") & Chr(13) & Chr(10). In that expressions appears string constants (enclosed between “) concatenated (by intermediate of & operator) with the result of evaluation of string (character, text) manipulation functions (as Chr, String). The character _ (underscore) appearing on line 6 instruct the compiler (or interpreter) that the command line is continued to the line that follows;
Line 7 it introduces a processing cycle that expressed in a natural language as: For the variable named fahrenheit starting with the value min (fahrenheit=min) To value max, with a Step equal to s (from step by step) execute the instructions from the lines that follows until the program line containing the sentence to repeat (Next fahrenheit, line 10). The execution ends when the value of fahrenheit is greater than max. To each executed cycle the value of s is added to the variable fahrenheit.
Line 8 transforms the Fahrenheit degrees in Celsius degrees;
Line 9 transform the computed values in a character string by using string functions and complete a table line.
top
We want to keep the marks obtained by a student over 5 years of studies in tables of the form:
Student First name & Last name |
Studies Year |
Obtained Marks |
Discipline 1 |
Discipline 2 |
… |
Discipline 10 |
I |
|
|
|
|
II |
|
|
|
|
III |
|
|
|
|
IV |
|
|
|
|
V |
|
|
|
|
In the table below, on the rows numbered from I to V, the studies years are enumerated, and on columns we have ten disciplines, representing the disciplines from each year.
By the notation Mark 1,5 we define the mark obtained in the first year to the discipline 5. This table can be represented in computer as a bidimensional array or matrix. If we denote by i and j two variables by which we designate a line (i), and respectively a column (j) from the table then by Mark i, j we designate the mark obtained in the year i to the discipline j.
The computation formula (or the algorithm) used to determine the average is:
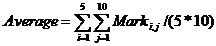
The sum of all marks from the table is computed by adding the value Marki,j to the sum obtained by adding the previous values (by following the way: after each adding operation we obtain a subtotal to which the next value is added).
The computation program can be:
Sub Average_Marks()
An output sample |
Dim Mark(5, 11), i As Integer, j As Integer: Rem the definition of the table in the internal memory
Dim Average As Double, Name As Variant
Read_Marks Name, Mark
Average = 0
For i = 1 To 5
For j = 1 To 10
Average = Average + Average(i, j)
Next j
Next i
Average = Average / (10 * 5)
MsgBox "Studentul " & Name & Chr(13) & Chr(10) & "are media generala: " & Average
End Sub
In the table Mark, we must fill, in each cell (called element) the obtained Mark. We fill the marks by reading them from a file where previously stored or from the keyboard. The table defined by the sentence Dim Mark(5,10) is called usually matrix, bidimensional array or bidimensional massive.
In this example the procedure Read_Marks is defined as follows:
Sub Read_Marks(Name As Variant, Mark As Variant)
Name = InputBox("First Name & Last Name:", "Example of using VB")
For i = 1 To 5
For j = 1 To 10
Mark(i, j) = InputBox("Name:" & Name & Chr(13) & Chr(10) & _
"Mark: (" & i & " , " & j & " ) ", "Example of using VB: Marks Input")
Next j
Next i
End Sub
top
COPYRIGHT© 2006-2009 Vasile AVRAM.


![]() Visual
Basic Code Examples
Visual
Basic Code Examples



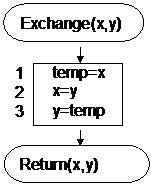

 Figure 5 A flowchart for the Newton-Raphson method
Figure 5 A flowchart for the Newton-Raphson method







